Rotational Kinematics

Moment of Inertia

1. What I knew

Moment of inertia is the name given to rotational inertia, the rotational analog of mass for linear motion. It appears in the relationships for the dynamics of rotational motion.

2. What I learned

• Moment of inertia (I) is always specified with respect to that axis and is defined as the sum of the products obtained by multiplying the mass of each particle of matter in a given body by the square of its distance from the axis.

For a point mass orbiting a point a distance r away, its moment of inertia is:

~We measure moment of inertia in kg · m², a weighted assessment of mass by distance.
If there are a whole bunch of point masses rotating, their collective moment of inertia is just the sum of all the object’s individual moments of inertia:

Example:
By applying some calculus magic, we can take this sum-of-its-parts aspect of moment of inertia and figure out I for complicated rigid bodies, such as spheres or cylinders. Case in point for even the non-calculus inclined: the hula hoop.

Imagine the hula hoop as made of very, very small chunks of hoop, each of mass m, and glued together:

~As you hula, each hoop chunk spins around at the same radius r (the radius of the hula hoop). Then each hoop chunk has a moment of inertia around this axis of rotation of I_chunk = mr². The moment of inertia of the hoop is the sum of all the chunks: I_hoop = m₁r² + m₂r² + m₃r² + …= Mr², where

is the overall mass of the hoop.
The same process works for disks, rods, cubes—but the summation process is a little more involved. Here’s a breakdown of some common shapes: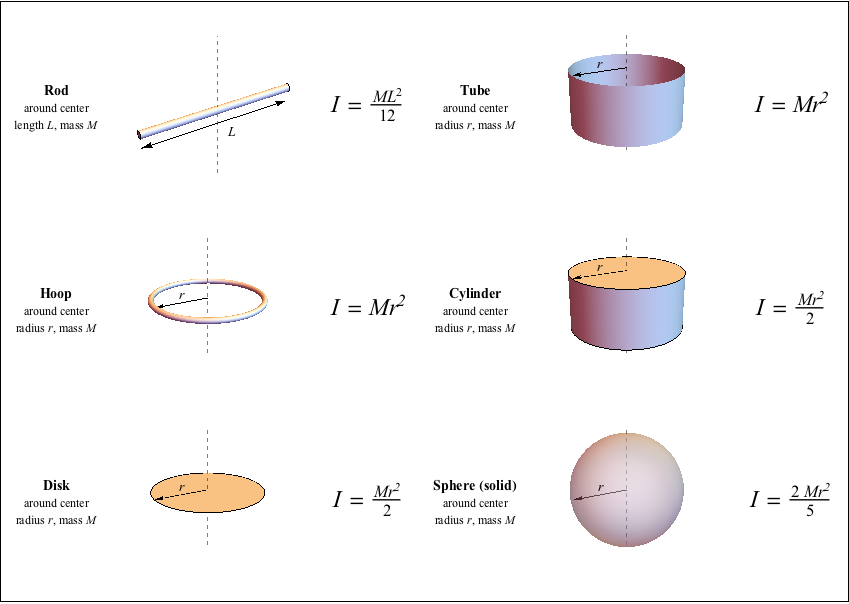

• The moment of inertia of a point mass with respect to an axis is defined as the product of the mass times the distance from the axis squared. The moment of inertia of any extended object is built up from that basic definition. The general form of the moment of inertia involves an integral.

Moment of Inertia, General Form

~Since the moment of inertia of an ordinary object involves a continuous distribution of mass at a continually varying distance from any rotation axis, the calculation of moments of inertia generally involves calculus, the discipline of mathematics which can handle such continuous variables. Since the moment of inertia of a point mass is defined by

then the moment of inertia contribution by an infinitesmal mass element dm is given by

The sum over all these mass elements is called an integral over the mass.

Usually, the mass element dm will be expressed in terms of the geometry of the object, so that the integration can be carried out over the object as a whole (for example, over a long uniform rod).

3. How I Learned

*HOW TO CALCULATE THE MOMENTUM OF INERTIA FOR DIFFERENT SHAPES AND SOLIDS

• Measure the distance r from any particle in the object to the axis of symmetry
• Square that distance
• Multiply that squared distance times the mass of the particle
• Repeat for every particle in the object
• Add all of these values up

~In physics, when you calculate an object’s moment of inertia, you need to consider not only the mass of the object but also how the mass is distributed. For example, if two disks have the same mass but one has all the mass around the rim and the other is solid, then the disks would have different moments of inertia.
Calculating moments of inertia is fairly simple if you only have to examine the orbital motion of small point-like objects, where all the mass is concentrated at one particular point at a given radius r. For instance, for a golf ball you’re whirling around on a string, the moment of inertia depends on the radius of the circle the ball is spinning in:

I = mr²

Here, r is the radius of the circle, from the center of rotation to the point at which all the mass of the golf ball is concentrated.

Crunching the numbers can get a little sticky when you enter the non–golf ball world, however, because you may not be sure of which radius to use. What if you’re spinning a rod around? All the mass of the rod isn’t concentrated at a single radius. When you have an extended object, such as a rod, each bit of mass is at a different radius. You don’t have an easy way to deal with this, so you have to sum up the contribution of each particle of mass at each different radius like this:

You can use this concept of adding up the moments of inertia of all the elements to get the total in order to work out the moment of inertia of any distribution of mass. Here’s an example using two point masses, which is a bit more complex than a single point mass. Say you have two golf balls, and you want to know what their combined moment of inertia is. If you have a golf ball at radius r₁ and another at r₂, the total moment of inertia is

~So how do you find the moment of inertia of, say, a disk rotating around an axis stuck through its center? You have to break the disk up into tiny balls and add them all up. You complete this using the calculus process of integration.

The shapes corresponding to the moments of inertia in the table.

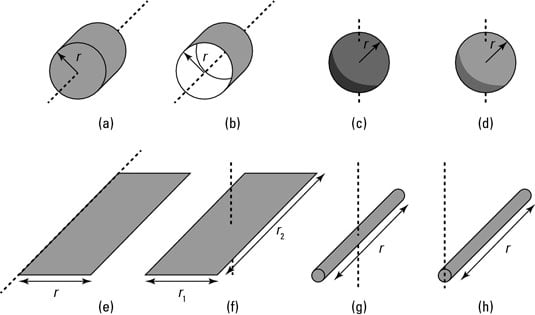
Trusty physicists have already completed this task for many standard shapes; The following table provides a list of objects you’re likely to encounter, and their moments of inertia. The figure depicts the shapes that these moments of inertia correspond to.

* VIDEO

This video talked about the moment of inertia in every objects that we used in performing or feeling the moment of inertia. The moment of inertia of an object is a calculated quantity for a rigid body that is undergoing rotational motion around a fixed axis. It is calculated based upon the distribution of mass within the object and the position of the axis, so the same object can have very different moment of inertia values depending upon the location and orientation of the axis of rotation.
For example, how hard is it to rotate a particular object (move it in a circular pattern relative to a pivot point)? The answer depends on the shape of the object and where the object’s mass is concentrated. So, for example, the amount of inertia (resistance) is fairly slight in a wheel with an axis in the middle. All the mass is evenly distributed around the pivot point. It’s much greater, though, in a telephone pole that you’re trying to rotate from one end.

4. Reflection

The Importance of Inertia in Person’s Life

Concepts you’ve learned in the past are stored in your subconscious, waiting for just the right moment to influence your life. These moments serve as a reminder that often we go through life hearing when we should be listening. Take for instance Sir Isaac Newton’s first universal law of motion which beforehand I was only hearing but just now began to listen:

“An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.”
To keep it simple, this law of motion can be summed up into one word: inertia — the natural tendency of objects to resist changes to their current state.
The concept of inertia holds much truth, but on a grander scale than science alone. This concept lends itself applicable to one’s own life direction.
Momentum is powerful. At times, life’s momentum can feel as if it’s speeding up and taking over. Perhaps leading us further and further down a path we might not believe in. This path might be the path of others, perhaps even the path of people who you care for and who care for you, but you know deep down that it’s not yours.
Where the analogy between the law of motion and life’s momentum ends is in one obvious loophole: we are not objects — we’re humans. We have the power of choice and the control over our own free will to combat inertia. The fact is, is that no matter how many forces might be acting upon us at a given time, the only force that should decide your present self is your own.
Often, we stand hesitant, waiting for outside forces to come in and take us in a new direction. In our relationships and careers… we’re always waiting. Waiting for these forces to guide us into better situations and out of worse ones.
Leverage the following steps to aid in propelling yourself into the right direction (much like a business might determine its own direction):

1. analyze the unexplored, desired inertia (develop mission/vision, market research, R&D)
2. experience the inertia (implement, execute, market)
3. evaluate the explored inertia (review consumer feedback loops, goals and statements)
4. continue or discontinue the momentum (reinvest, or adapt/pivot/divest)

Please stop waiting. Only you have the forces necessary to guide your life’s momentum. Assess your inertia. Do not stay at rest, but do not travel down a path that’s not yours. If you’re going to let life’s motion build momentum, make sure it’s by your own choice.
Likewise, if you’ve identified your inertia is desired, keep riding that wave. You’re right where you need to be.

Analogs of Rotational Motion

1. What I knew

Rotational Motion 

~the motion of a rigid body which takes place in such a way that all of its particles move in circles about an axis with acommon angular velocity; also, the rotation of a particle about a fixed point in space

2. What I learned

~If a body is pivoted at a point and the force is applied on the body at a suitable point, it rotates the body about the axis passing through the pivoted point. This is the turning effect of the force and the motion of body is called the Rotational motion.
We can say circular motion can be analyzed in the same way of linear motion. In this unit, we will examine the motion of the objects having circular motion.
For example, we will find the velocity, acceleration and other concepts related to the circular motion in this section. Uniform circular motion is one of the example of this subject. In uniform circular motion speed of the object is always constant and direction is changing. Thus, velocity of the object is changing and as a result object has acceleration. Some concepts will be covered in this units; rotational speed (angular speed), tangential speed (linear speed), frequency, period, rotational inertia of the objects, torque, angular momentum and its conservation.

Tangential Speed Velocity with Examples

• Linear Speed (Tangential Speed)

Linear speed and tangential speed gives the same meaning for circular motion. In one dimension motion we define speed as the distance taken in a unit of time. In this case we use again same definition. However, in this case the direction of motion is always tangent to the path of the object. Thus, it can also be called as tangential speed, distance taken in a given time. Look at the given picture and try to sequence the velocities of the points larger to smaller.

~In a given period of time all points on this rotating object have same revolutions. In other words, if A completes one revolution, then B and C also have one revolution in a same time. The formula of the speed in linear motion is;

Speed=distance/time

As I said before, speed in circular motion is also defined as the distance taken in a given time. Thus, speeds of the points given in the picture above are;

V =Distance/time: If the object has one complete revolution then distance traveled becomes; 2πr which is the circumference of the circle object.

VA=2πr/time

Period: Time passing for one revolution is called period. The unit of period is second. Tis the representation of period.

The equation of tangential speed becomes; VA=2πr/T

Frequency: Number of revolutions per one second. The unit of frequency is 1/second. We show frequency with letter f.

The relation of f and T is; f=1/T

Now; with the help of the information given above lets’ sequence the velocities of the points on given picture.

Since the velocity or speed of the points on rotating object is linearly proportional to the radius r3>r2>r1; V3>V2>V1

~To sum up, we can say that tangential speed of the object is linearly proportional to the distance from the center. Increase in the distance results in the increase in the amount of speed. As we move to the center speed decreases, and at the center speed becomes zero. We use the same unit for tangential speed as linear motion which is “m/s”.

Example: A particle having mass m travels from point A to B in a circular path having radius R in 4 seconds. Find the period of this particle.

~Particle travels one-fourth of the circle in 4 seconds. Period is the time necessary for one revolution. So,

T/4=4s

T=16s.

Example: If the particle having mass m travels from point A to B in 4 seconds find the tangential velocity of that particle given in the picture below. (π=3)

~We first find the period of the motion. If the particle travels half of the circle in 4 seconds;

T/2=4s

T=8s

v=2 π R/T

v=2.3.3m/8s=9/4 m/s tangential speed of the particle

Angular Velocity with Examples

• Angular Velocity

Look at the given picture. If the platform does one rotation then points A and B also does one rotation. We define angular velocity as “change of the angular displacement in a unit of time”. the unit of angular velocity is revolution per unit time or radians per second. We show angular velocity with the Greek letter “ω” omega.

Average Velocity= Circumference of the Circle/Time

Average Speed/Velocity=2πr/T where, T is the period of the system and r is the radius of the revolution.

ω=2π/T=2πf where, f is frequency and T is the period

Unlike tangential velocity, angular velocity of all points on the platform doing circular motion are equal to each other since the number of rotations per unit time are equal.

Example: If the stone does 6 rotations in 1 second find the angular velocity of it.

~If the stone does four rotations in one second then its frequency becomes 6.

f=6s^-1

T=1/f=1/6s

ω=2π/T=2.3/1/6s=36radian/s

TORQUE WITH EXAMPLES

• Torque

~We define torque as the capability of rotating objects around a fixed axis. In other words, it is the multiplication of force and the shortest distance between application point of force and the fixed axis. From the definition, you can also infer that, torque is a vector quantity both having direction and magnitude. However, since it is rotating around a fixed axis its direction can be clockwise or counterclockwise. During the explanations and examples we give the direction “+” if it rotates clockwise direction and “–” if it rotates counterclockwise direction. Torque is shown in physics with the symbol “τ”. You can come across torque with other name “moment”. Now, we examine given pictures one by one to understand torque in detail.

How can we find the shortest distance between the applied force and fixed axis?
~All we know that, a shortest distance between two points is the straight line connecting them. In this situation distance connecting these two points is the length of the object. The direction of the torque is “+” because force rotates the object in a clockwise direction. (We ignore the weight of the object n all situations given above.)

Thus, we can write the torque equation like;

Τ=Applied Force.Distance

~In this picture, we have a different situation where the object is fixed to the wall with an angle to the horizontal. Direction of the torque in this situation is “-” because force rotates the object in counterclockwise direction. As we said before we need shortest distance between the force and turning point. Dashed line in the picture shows this distance which can be found by using trigonometry and final equation of torque becomes;

Τ=Applied Force.Distance.sinΘ

Final situation shows that, if the extension of the force is passing on the rotation axis then what would be the torque?

~I want to explain this situation by giving other example. Think that you are opening a door. If you push the door as in the case of given picture above, the door does not move. However, if you apply a force to the door like in the first and second situations given above the door is opened or closed. What I try to say is, if the force is applied to the turning point then it does not rotate the object and there won’t be torque.

Example: If the given triangle plate is fixed from the point O and can rotate around this point, find the total torque applied by the given forces.

Example: If the plate is fixed from the point O, find the net torque of the given forces.

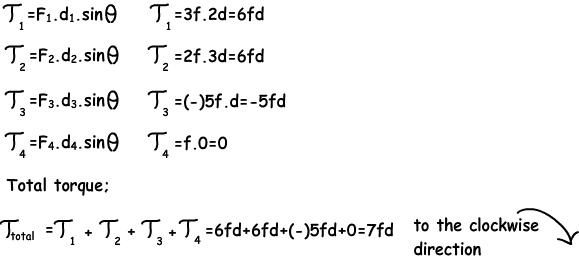
~Doorknobs, wrenches, even nail clippers: they’re all methods of applying a force at a point other than where you turn the nob, grab the wrench, or pinch the clippers. This idea—force applied at a distance is called torque.
Torque shows up in many different forms throughout many fields of physics. Imagine a mobile hanging from the ceiling, with one large weight and two small weights:

You’d think, given the large weight on the left and the small weights on the right, the mobile would rotate—pivot counterclockwise, dragged down by the heavy weight. But in fact, the mobile is perfectly balanced. That’s torque—even a small force (such as the weight of a light mobile component) can cancel out a large force given a large enough lever arm to act over. For a mobile, the lever arm each weight acts over is literally an arm; for a wrench, it’s the length of the handle; for a doorknob, the width of the door.
~Torques will always try to rotate objects, the same way a force will try to translate an object. In the mobile example, the force of gravity on each hanging weight tries to pull the mobile down to the ground, but each force is canceled by an equal and opposite reaction force at the attachment point to the ceiling.

~To prevent the mobile from rotating, the torques must also be balanced. The long lever arm of the light weights, the distance between the light weights and the point the mobile would rotate about. It means they create the same net torque as the heavy weight with a shorter lever arm.

When both forces and torques are balanced, an object cannot move. This is called static equilibrium and is the goal of every architect and bridge builder on the planet.

Other examples:
Try to push to open a door using the doorknob, the heavier the door the better (don’t pull or else the next step won’t make much sense), and this time, unlatch the door, but don’t push it open with the doorknob. Instead, put your hand near the hinges and push the door open.
~Much harder the second time, right? That’s because even though you’re applying the same force, the longer lever arm you get by pushing on the knob instead of near the hinge greatly increase the torque on the door, making it easier to swing open.

We capture this by defining a torque as the perpendicular product of force and distance. In other words, for a force F applied a distance r away from the rotation point of an object, the torque (τ) created is:

~Torque is measured in newton-meters. θ is the angle between the direction of the force and the direction of r. The maximum amount of torque—maximum amount of potential rotation creation—occurs when

(or, fine, 90°) since

. Any other angle decreases the sinθ term and so decreases τ.

• Newton’s Second Law

The kinematics equations we learned for translational motion had direct rotational analogs, and Newton’s Second Law does, too. Newton’s Second Law for translational motion is the one in between the first commandment and third amendment, and goes a little something like this:

F = ma

Essentially F = ma says that the larger the mass of an object m, the more force F you need to accelerate it at the same rate a. Rotationally, the same thing holds—except when we’re talking about rotation, we don’t use a. We use α. Newton’s Second Law for rotation states that the harder an object is to turn, the more torque is needed to accelerate it at the same angular rate. Or, if you prefer your analogies to be neat and tidy:

τ = Iα

~I is the rotating object’s moment of inertia, or its resistance to rotation—exactly as mass, m, is a measure of an objects resistance to translational motion. Two points science.

Common Mistakes

Torque is a product of force and distance—but also a function of the angle between force and distance. Don’t forget the sin θ in τ = rF sin θ.

* Technically, 1 N · m = 1 kg · m²/s² = 1 J. We tend to keep this hush-hush and keep on referring to energy in J and torque in N · m. Remember this unit coincidence when we get to the section on rotational work, however.

3. How I Learned

~The motion of objects as they translate — move bodily from one place to another — follows a simple set of rules. It turns out that a very similar set of rules describes the motion of objects as the rotate — spin around in place.

~Physicists usually don’t use degrees as a unit to measure angles. Instead, they use radians, which are ratios of the arc length described by an angle to the radius of the arc:

                               length of arc
          angle in radians =  ---------------
                                 radius

There are 2*pi = 6.28 radians in one full revolution. Therefore

                2 * pi radians =  360 degrees

–> 1 radian = 57.3 degrees
Each translational quantity has a rotational analog:

      displacement (meters)       -->     angular displacement (radians)

velocity (meter/sec) –> angular velocity (radian/sec)

acceleration (meter/sec^2) –> angular acceleration (radian/sec^2)

~These rotational quantities obey a set of kinematic equations, exactly analogous to the 1-D translational kinematic equations.

• Rotational Motion Vs Translational Motion

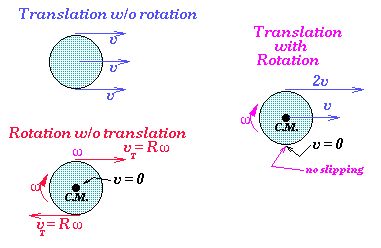
~Usually linear velocity is the velocity of a point rotating around the axis of rotation given by v⃗ =ω⃗ ×r⃗ v→=ω→×r→ when object has no translational motion but if the object has both translational and rotational motion then v⃗ v→ will be measured from center-of-momentum frame. In the frame where the C.M is translating at velocity v⃗ C.Mv→C.M the velocity of any point P revolving at angular velocity ω⃗ ω→ can be found by using Galilean transformation i.e v⃗ ′=v⃗ +vC.M→v→′=v→+vC.M→. (assuming v,vC.M<<cv,vC.M<<c)
~In the case point P is moving in the direction that is opposite to the direction of motion of C.M that’s why subtraction is being done, if P was moving in the same direction as that of vC.MvC.M then addition would have been done.
Suppose we have a particle moving with a velocity v⃗ 1v→1 and a object which has no linear velocity, but is rotating with angular velocity ω⃗ ω→. Now suppose we look at a point at a displacement r⃗ r→ from the axis of rotation of this rotating velocity. The velocity of this point is v⃗ 2=ω⃗ ×r⃗ v→2=ω→×r→.

Now the velocity of the first object relative to the point on the disc is the difference of these two velocity. This makes sense because if they are moving with the same velocity then the relative velocity is zero. Thus we find v⃗ rel=v⃗ 1−v⃗ 2=v⃗ 1−ω⃗ ×r⃗ v→rel=v→1−v→2=v→1−ω→×r→.

Related Video:

Difference Between Translational and Rotational Motion

Translational motion involves objects moving through space, while rotational motion involves objects changing orientation.

Here’s an example: Imagine a pencil pointing up. If you throw that pencil, it would be translated. You are causing it to move through space. If you were to keep the pencil in the same position, however, but turn it so it is pointing down, it would be rotated. You are causing it to change orientation.

• Determine the Rotational Motion of an Objects

~The picture below was an activity on how we determine the rotational motion of the objects like a can and a ball of golf. We can see that the can has greater mass than the ball of golf. The golf has lesser amount of mass than a can and the rotation of the objects, and if we talked about the speed of the objects the can has more amount of speed than the ball of golf.

4. Reflection

 

Summary

Rotational motion of a rigid body which takes place in such a way that all of its particles move in circles about an axis with acommon angular velocity; also, the rotation of a particle about a fixed point in space. Rotational motion is illustrated by (1) thefixed speed of rotation of the Earth about its axis; (2) the varying speed of rotation of the flywheel of a sewing machine; (3)the rotation of a satellite about a planet; (4) the motion of an ion in a cyclotron; and (5) the motion of a pendulum. Circularmotion is a rotational motion in which each particle of the rotating body moves in a circular path about an axis. Such motionis exhibited by the first and second examples. For information concerning the other examples See Harmonic motion, Particle accelerator, Pendulum

The speed of rotation, or angular velocity, remains constant in uniform circular motion. In this case, the angular displacementΘ experienced by the particle or rotating body in a time t is Θ = ωt, where ω is the constant angular velocity.

A special case of circular motion occurs when the rotating body moves with constant angular acceleration. If a body ismoving in a circle with an angular acceleration of α radians/s², and if at a certain instant it has an angular velocity ω₀, then ata time t seconds later, the angular velocity may be expressed as ω = ω₀ + αt, and the angular displacement as Θ = ω₀t +½αt². See Acceleration, Velocity

A rotating body possesses kinetic energy of rotation which may be expressed as T_rot = ½Iω², where ω is the magnitude ofthe angular velocity of the rotating body and I is the moment of inertia, which is a measure of the opposition of the body toangular acceleration. The moment of inertia of a body depends on the mass of a body and the distribution of the massrelative to the axis of rotation. For example, the moment of inertia of a solid cylinder of mass M and radius R about its axis ofsymmetry is ½MR².

The action of a torque L is to produce an angular acceleration α according to the equation below, where Iω, the product

of moment of inertia and angular velocity, is called the angular momentum of the rotating body. This equation points out thatthe angular momentum Iω of a rotating body, and hence its angular velocity ω, remains constant unless the rotating body isacted upon by a torque. Both L and Iω may be represented by vectors.

It is readily shown that the work done by the torque L acting through an angle Θ on a rotating body originally at rest is exactlyequal to the kinetic energy of rotation. See Angular momentum, Moment of inertia, Rigid-body dynamics, Torque, Work

 

Rotational Motion Example Problems

Problem 1:

Wheel A of radius r_A = 10.0 cm is coupled by a belt b to wheel C of radius r_C = 25.0 cm, as shown in below figure. Wheel A increases its angular speed from rest at a uniform rate of 1.60 rad/s². Determine the time for wheel C to reach a rotational speed of 100 rev/min, assuming the belt does not slip. (Hint: If the belt does not slip, the linear speeds at the rims of the two wheels must be equal).

Concept: Assume that desired angular speed of wheel C is ω_C and the angular velocity of wheel A corresponding to angular speed of wheel C is ω_A.

The belt rolls without slipping, therefore the tangential speed of the wheel must be equal, that is v_TA = v_TC

Here v_TA is the tangential speed of wheel A and v_TC is the tangential speed of wheel C.

The above equation can also be written as:

r_Aω_A = r_C ω_C

ω_A = (r_C ω_C) /r_A

The time taken by wheel A to attain the angular speed of ω_A is equal to the time taken by wheel C to attain the angular speed ω_C. Therefore if the wheel has an angular acceleration say α, the time taken by the wheel A to move from rest to ω_A is:

α = ω_A/t

t = ω_A/ α

Substitute ω_A = (r_C ω_C) /r_A in the equation t = ω_A/ α,

~Therefore the time taken by wheel C to attain the angular speed of ω_C is t =(r_C ω_C) /αr_A.

Solution:

Substitute r_A = 10.0 cm, r_C = 25.0 cm, α = 1.60 rad/s² and ω_C = 100 rev/min in equation t = (r_C ω_C) /αr_A,

Round off to three significant figures,

t = 16.4 s

~Therefore the time taken by wheel C to attain the angular speed of 100 rev/min is 16.4 s.

Problem 2:

Below figure shows a uniform block of mass, M and edge lengths a, b, and c. Calculate its rotational inertia about an axis through one corner and perpendicular to the large face of the block.

Concept: Use the rotational inertia of the uniform block about the axis passing through its center and normal to the plane, as shown in the diagram above:

The rotational inertia say I of the block about the axis shown in figure above is

1/12 [M (a²+b²)].

Therefore the rotational inertia (say I ‘) about the axis through one corner and perpendicular to the large face can be calculated using the parallel axis theorem as: I ‘= I+Mh²

Here h is the perpendicular distance between the both the axis (refer figure below)

Solution:

The distance h is given as:

~Therefore the moment of inertia of the uniform block about the axis through one corner and perpendicular to large face of the block is M (a² + b²)/3.

Problem 3:

A top is spinning at 28.6 rev/s about an axis making an angle of 34.0º with the vertical. Its mass is 492 g and its rotational inertia is 5.12×10^-4 kg.m². The center of mass is 3.88 cm from the pivot point. The spin is clockwise as seen from above. Find the magnitude (in rev/s) and direction of the angular velocity of precession.

Concept: The angular velocity of the precession of the spinning top is given as:

ω _p = Mgr/L

Here L is the angular momentum of the spinning top, M is the mass of the spinning top, g is the acceleration due to gravity and r is the distance between the origin and the point at the top.

Also, the angular momentum of the spinning top can be written as L=Iω. Substitute the value of angular momentum in equation ω _p = Mgr/L,

ω _p = Mgr / Iω

Here ω is the angular velocity of the spinning top and I its rotational inertia.

Solution:

Substitute 492 g for M, 9.81 m/s² for g, 3.88 cm for r, 5.12×10^-4 kg.m² for I and 28.6 rev/s for ω in equation ω _p = Mgr / Iω,

~Therefore, the angular velocity of the precession of the spinning top is 0.324 rev/s.

The figure below shows the spinning top and the direction of the angular velocity of precession.

It can be seen from the figure that the direction of ω _p is perpendicular to the plane of cone.

Problem 4:

A deep-sea fisherman hooks a big fish that swims away from the boat pulling the fishing line from his fishing reel. The whole system is initially at rest and the fishing line unwinds from the reel at a radius of 4.50 cm from its axis of rotation. The reel is given an angular acceleration of 110 rad/s² for 2.00 s as seen in Figure 1. (a) What is the final angular velocity of the reel? (b) At what speed is fishing line leaving the reel after 2.00 s elapses? (c) How many revolutions does the reel make? (d) How many meters of fishing line come off the reel in this time?

Solution

(a) Here α and t are given and ω needs to be determined. The most straightforward equation to use is ω = ω₀+αt because the unknown is already on one side and all other terms are known. That equation states that

ω = ω₀ + αt.

We are also given that ω₀ = 0 (it starts from rest), so that

ω = 0 + (110 rad/s²)(2.00 s) = 220 rad/s
(b) Now that ω is known, the speed v can most easily be found using the relationship

v = rω,

where the radius r of the reel is given to be 4.50 cm; thus,

v = (0.0450 m)(220 rad/s) = 9.90 m/s.

Note again that radians must always be used in any calculation relating linear and angular quantities. Also, because radians are dimensionless, we have m × rad = m .
(c) Here, we are asked to find the number of revolutions. Because 1 rev=2π rad, we can find the number of revolutions by finding θin radians. We are given α and t, and we know ω₀ is zero, so that θ can be obtained using $\theta ={\omega }_{0}t+\frac{1}{2}{\alpha t}^2$.
$\begin{array}{ccc}\theta & =& {\omega }_{0}t+\frac{1}{2}{\alpha t}^2\\ =& 0+\left(\text{0.500}\right)\left(\text{110}{\text{rad/s}}^2\right){\left(\text{2.00 s}\right)}^2=\text{220 rad}.\end{array}$

Converting radians to revolutions gives
$\theta =\left(220\text{rad}\right)\frac{1\text{rev}}{2\pi \text{rad}}=35.0\text{rev}$
(d) The number of meters of fishing line is x, which can be obtained through its relationship with θ:

x = rθ = (0.0450 m) (220 rad) = 9.90 m.